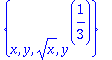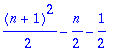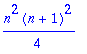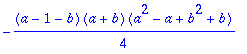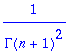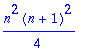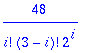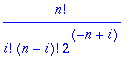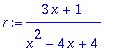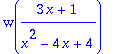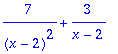introMaple.mws
A Short Introduction to Maple
Arithmetic Operations
Variable Assignement
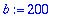

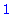
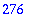
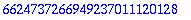
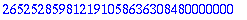
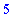
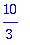
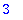
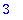
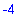
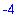
| > |
floor(2.3); floor(-2.3);
|
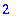
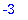
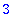
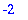
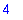
Quotes, Concatenation operator
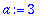
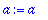
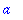
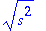
| > |
assume(s>0); sqrt(s^2);
|
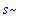
| > |
assume(s<0); sqrt(s^2);
|
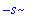
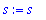
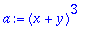
In Maple 5, the concatenation operator was the dot.
In Maple 6, the concatenation operator is the two vertical bars.
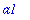
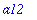
Definition of strings
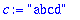
Interface, Code Generation
Customize the user interface
| > |
interface(screenwidth=100);
|
| > |
interface( quiet=true);
|
| > |
interface( quiet=false);
|
| > |
interface( verboseproc = 2 );
|
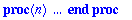
LaTeX interface
| > |
expr:=expand((x+y)^10);
|
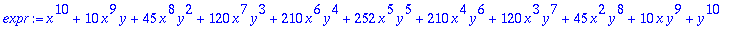
{x}^{10}+10\,{x}^{9}y+45\,{x}^{8}{y}^{2}+120\,{x}^{7}{y}^{3}+210\,{x}^{6}{y}^{4}+252\,{x}^{
5}{y}^{5}+210\,{x}^{4}{y}^{6}+120\,{x}^{3}{y}^{7}+45\,{x}^{2}{y}^{8}+10\,x{y}^{9}+{y}^{10}
C and Fortran code generation
Warning, the protected name MathML has been redefined and unprotected
| > |
C(1-x/2+3*x^2-x^3+x^4);
|
t0 = 1.0-x/2.0+3.0*x*x-x*x*x+x*x*x*x;
| > |
fortran(1-x/2+3*x^2-x^3+x^4);
|
t0 = 1-x/2+3*x**2-x**3+x**4
| > |
C([a=10.3*x-y,b=z/t*log(z)]);
|
a = 0.103E2*x-y;
b = z/t*log(z);
| > |
fortran([a=10.3*x-y,b=z/t*log(z)]);
|
a = 0.103D2*x-y
b = z/t*log(z)
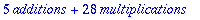
Types (whattype, type, hastype)
Maple has a type system. Using it is not obligatory though.
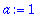
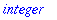
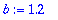
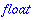
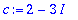

| > |
c:=cos(x); whattype(c);
|
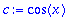
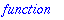
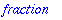
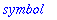
For lazy typists, there is an alias mechanism in Maple.
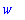
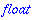
| > |
w(x+y); w(x*y); w(x^3);
|


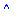
Besides whattype, there are two more commands that handle types
| > |
type(a,integer); type(b,integer);
|
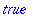
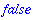
| > |
hastype(a,integer); hastype(b,integer);
|
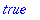
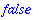
The hastype(expr,t) returns true if expr has a subexpression of the type t
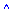
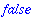
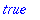
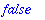
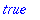
| > |
pol:=expand((x+x*y)^2);
|
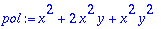

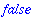
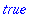
Access parts of a Maple expression (op, nops, indets)
Tree structure of an expression in Maple.
Internal representation of mathematical expressions.
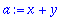
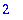
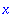
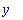
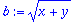
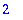
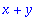
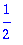
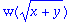
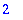
| > |
op(1,op(2,b)); op(2,op(2,b));
|
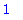
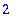
Because fractions are quite common,
there are two special commands to get
the numerator and the denominator.
| > |
numer(1/2); denom(1/2);
|
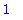
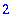
There is a more compact way to write this
| > |
op([2,1],b); op([2,2],b);
|
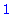
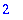
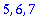
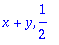
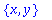
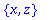
| > |
indets(sqrt(x)); nops(sqrt(x));
|
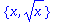
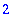
| > |
indets(sqrt(x)+y^(1/3));
|
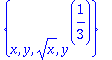
| > |
indets(exp(x+y)); indets(log(x+y));
|
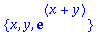
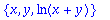
Sequences, Lists and Sets
A sequence is defined as a succession of elements separated by commas
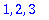

We can create fairly complicated sequences
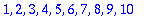
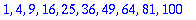
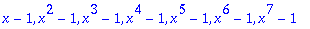
A
list
is defined as a sequence enclosed in (square) brackets
![l := [1, 2, 3]](images/introMaple97.gif)
You can use
seq
to define new lists
| > |
l:=[seq(ifactor(i),i=1..6)];
|
![l := [1, ``(2), ``(3), ``(2)^2, ``(5), ``(2)*``(3)]](images/introMaple99.gif)
To access the i-th element of a list
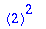
A
set
is defined as a sequence enclosed in (curly) braces
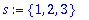
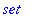
Sets cannot contain multiple elements as opposed to lists
![l := [1, 1, 2, 3]](images/introMaple103.gif)
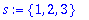
Apply a function to every element of a list (map)
![l1 := [1, 9, 64]](images/introMaple105.gif)
![[1, 3, 8]](images/introMaple106.gif)
![l2 := [-1, 4, -6]](images/introMaple107.gif)
![[1, 4, 6]](images/introMaple108.gif)
![l3 := [10/3, 2, 3/7]](images/introMaple109.gif)
![[3.333333333, 2., .4285714286]](images/introMaple110.gif)
![[3.33333333333333, 2., .428571428571429]](images/introMaple111.gif)
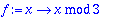
![[1, 1, 0]](images/introMaple113.gif)
| > |
map(x->x^2+1,[1,10,12]);
|
![[2, 101, 145]](images/introMaple114.gif)
| > |
map(x->x^3-1,[x,y+1,z+2]);
|
![[x^3-1, (y+1)^3-1, (z+2)^3-1]](images/introMaple115.gif)
![[(x-1)*(x^2+x+1), y*(y^2+3*y+3), (z+1)*(z^2+5*z+7)]](images/introMaple116.gif)
When the function has arguments,
these appear at the end.
| > |
l:=[1+x^2+x^2*y+x-x^2*y^3,x^3-x^3*y+x^2];
|
![l := [1+x^2+x^2*y+x-x^2*y^3, x^3-x^3*y+x^2]](images/introMaple117.gif)
![[1+(1+y-y^3)*x^2+x, (1-y)*x^3+x^2]](images/introMaple118.gif)
Operations on sets (union, intersect, member)
| > |
s1 := {1,2,3}; s2 := {1,4,5};
|
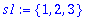
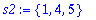
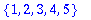
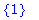
| > |
member(2,s1); member(2,s2);
|
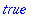
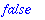
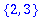
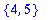
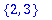
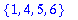
Operations on lists
Add an element to a list
![m1 := [1, 2, 3]](images/introMaple129.gif)
![m1 := [1, 2, 3, 4]](images/introMaple130.gif)
![m1 := [5, 1, 2, 3, 4, 6]](images/introMaple131.gif)
| > |
m1:=[op(1..3,m1),100,op(4..nops(m1))];
|
![m1 := [5, 1, 2, 100, 4, 6]](images/introMaple132.gif)
This technique is not efficient when
we are dealing with big lists.
Delete an element from a list
| > |
m2:= subsop(2=NULL,m1);
|
![m2 := [5, 2, 100, 4, 6]](images/introMaple133.gif)
Note that the initial list has been left unaltered.
m2 is a simply copy of m1, with the second element removed.
![[5, 1, 2, 100, 4, 6]](images/introMaple134.gif)
Modify an element of a list
![m1[2] := 20](images/introMaple135.gif)
![[5, 20, 2, 100, 4, 6]](images/introMaple136.gif)
![[5, 25, 2, 100, 4, 6]](images/introMaple137.gif)
![[5, 20, 2, 100, 4, 6]](images/introMaple138.gif)
Sums and Products (sum, prod)


sum looks for a closed form and then substitutes the
numerical values of the bounds of summations
add performs a loop from the lower bound to the upper bound
| > |
sum(i^2,i=1..1000000000000);
|

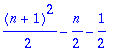
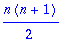
| > |
factor(sum(i^3,i=1..n));
|
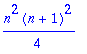
| > |
factor(sum(i^3,i=a..b));
|
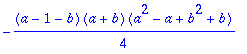
| > |
product(i,i=1..10); 10!;
|
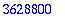
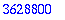
Infinite sums and products are handled
| > |
sum('1/i^2','i=1..infinity');
|
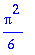
| > |
sum('1/k!', 'k'=0..infinity);
|

| > |
product('1-z^2/n^2','n=1..infinity');
|
product: "Cannot show that 1-z^2/n^2 has no zeros on [1,infinity]"
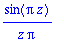
Sometimes the results are not immediately readable
| > |
product('1/i^2','i=1..n');
|
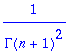
| > |
i:='i':k:='k':
sum(combinat[binomial](i+k-1,k-1),i=0..n);
|
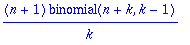
| > |
sum('(2*z)/(z^2-n^2)','n=1..infinity');
|
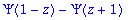
use single quotes to avoid premature evaluation
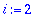
Error, (in sum) summation variable previously assigned, second argument evaluates to 2 = 1 .. 1000

in the following sum we access the command
binomial
from the
package
combinat
in the long form, avoiding the
with(combinat)
| > |
n:='n';
sum(combinat[binomial](n,k),k=0..n);
|
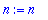
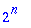
the sum is actually equal to (1+1)^n (binomial theorem)
we can have nested sums and products
| > |
factor(sum(sum('i*j','i=1..n'),'j=1..n'));
|
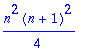
| > |
i:='i': j:='j': n:='2':
|
| > |
sum(sum(n!/(i!*j!*(n-i-j)!),i=0..n),j=0..n-i);
|
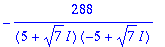

the sum is actually equal to (1+1+1)^2 = 9, by the trinomial theorem
now let us try to verify that (1+1+1)^3 = 27:
| > |
i:='i': j:='j': n:='3':
|
| > |
sum(sum(n!/(i!*j!*(n-i-j)!),i=0..n),j=0..n-i);
|
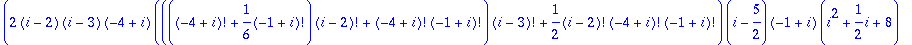
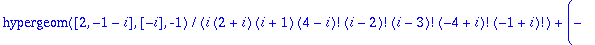
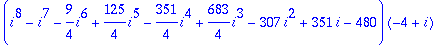
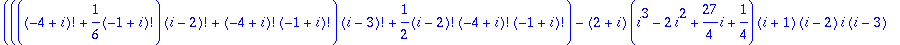
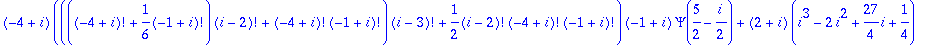
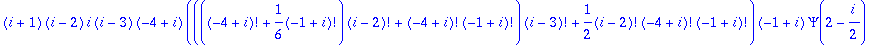
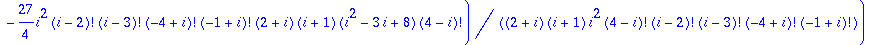
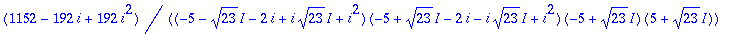
(more interesting things happen for n=4)
to actually do this sum we break it in two pieces
| > |
i:='i': j:='j': n:='3':
|
| > |
sum(n!/(i!*j!*(n-i-j)!),j=0..n-i);
|
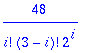
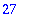
now we know how to do the general sum (1+1+1)^n = 3^n
| > |
i:='i': j:='j': n:='n':
|
| > |
sum(n!/(i!*j!*(n-i-j)!),j=0..n-i);
|
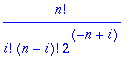
| > |
simplify(sum(%,i=0..n));
|
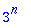
Conversions (convert)
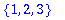
| > |
convert({1,2,3,4},list);
|
![[1, 2, 3, 4]](images/introMaple174.gif)
| > |
convert([1,1,2,3],set);
|
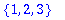
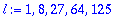
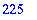
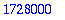
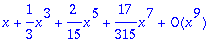
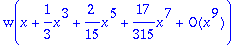
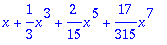
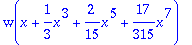
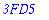
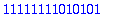

For more general bases, use the following syntax
![[1, 2]](images/introMaple186.gif)
![[0, 1]](images/introMaple187.gif)
Partial fraction decomposition of a rational function
| > |
r:=(3*x+1)/(x^2-4*x+4); w(r);
|
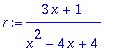
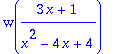
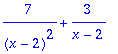
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()